InfoSec | CTF Challenges | CarolinaCon 2023 | smithy

This challenge (smithy) was one of the challenges in the cryptography category presented during the 2023 CarolinaCon CTF. The challenge provides a scenario description and three downloadable files.

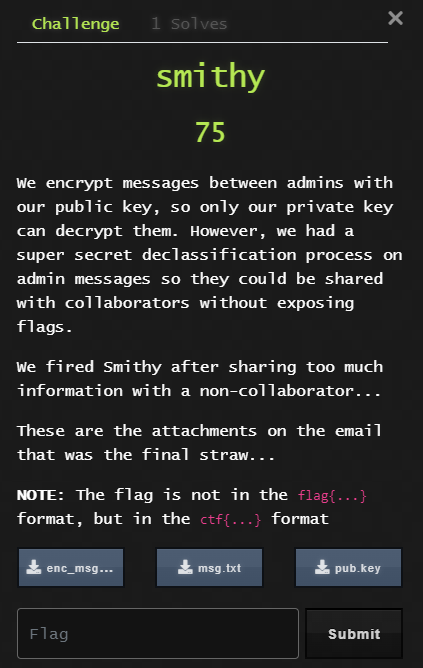
Scenario Description:

We encrypt messages between admins with our public key, so only our private key can decrypt them.

However, we had a super secret declassification process on admin messages so they could be shared with

collaborators without exposing flags.

We fired Smithy after sharing too much information with a non-collaborator...

These are the attachments on the email that was the final straw...

NOTE: The flag is not in the flag{...} format, but in the ctf{...} format

Downloadable Files:

enc_msg.txt - A text file that contains information that has been encrypted using the referenced public key

msg.txt - A text file that contains plain text with some redacted/masked characters

pub.key - A text file that contains the modulus and exponent of an RSA public key

File Contents:

enc_msg.txt

ŸnÕëì¿cNJƒiXšEKrÏûhœ¬âPŽ%ÌjÅä@éw¥Ï…ÛJ½Rì}Ÿ†ÔÀýå÷BI·íé©à½‚vÿଫÇîþ>¶_]lþzQ1bÅíe‹‡,í_ÍÈæpëwV?H(qcp-;™VµÄ2ƒÅØÖù{ª½³I‡T3æKŠºÓ‡
ý/ü\/·Œoƒ-$É83*`L—ŸÁIääI‘rLèF^O{;[Œzãc922üÙ^B W$ï="®òð.ÀcêH1 X©&KôÙ6†¨Äß÷([jlù©°`?„°PÂð—    R

msg.txt

Our flags are encrypted and classified, but the messages containing them can be declassified. For example, if we wanted to share this message, we have to remove the flag, like so: XXXXXXXXXXXXXXXXXXXX

pub.key

RSA Public-Key: (2048 bit)
Modulus:
  00:cc:4f:1e:56:4f:e2:d7:bf:10:dd:25:7c:24:ff:
  37:d0​:de:​c6:ba:c7:be:df:b2:a8:4f:cc:ed:97:c2:
  0b:58:14:aa:fd:ce:fc:02:07:f1:e6:73:03:d6:15:
  c3:39:fd:17:0b:e4:c3:7c:26:3b:49:fd:87:17:85:
  88:94:67:e9:4d:ed:ea:96:7e:75:26:1d:bf:d8:78:
  2c:08:71​:ab:​32:68:18:21:bd:b2:94:f8:ae:40:30:
  5d:4b:dc:82:b6:d8:e2:dc:9c:4f:27:dc:89:20:5f:
  99:1f:64:6b:c5:dd:ce:5c:45:46:8e:82:bc:19:9f:
  46:9a:27:11:91:81:b6:70:db:7b:3e:a1:16:1e:87:
  69:19:3a:2d:bd:e2:22:fe:93:32:76:3c:92:b7:25:
  fc:98:1e:34:23:b2:f6:e3:f5:b3:21:ff:5d:53:a0:
  c0:67:ce:c9:e4:6b:73:78:86:a3:f5:e0:80:e4:88:
  82:e4:dc:ff:7b:31:dd:fe:7f:35:02:59:30:f7:fc:
  85:d6:e0:e8:6a:e0:18:97:ae:7a:08:a9:f8:7f:13:
  f3:dc:e3:94:76:50:d9:fa:72:d0:0c:8c:3b:29:df:
  2f:ce:16:b2:3b:0c:0f:e1:5c:53:08:c9:ae:d4:f1:
  cf:14:e0:86:ff:7f:df:99:df:03:72:4d:27:86:b5:
  93:a7
Exponent: 7 (0x7)

Assessment:

The goal of this challenge is to reveal the flag which has been redacted from the end of the text in msg.txt.

The challenge has provided us with some important information which will enable us to accomplish the goal:

• A RSA public key modulus value

• A RSA public key exponent value

• Text that has been encrypted by the public key

• The number of characters which have been redacted in the plaintext message

With the information provided in the challenge, we can use the Coppersmith Method to obtain the flag.

We can do this, despite the flag's removal from msg.txt, because we can assume that msg.txt is the output of the stated "super secret declassification process on admin messages so they could be shared with collaborators without exposing flags."

Solution:

Before we can execute the Coppersmith Method and reveal the flag, we'll need a mathematics package which has an implementation of

Coppersmith's Method for univariate polynomials (otherwise we'd need to implement it ourselves). There are three packages which

include this implementation:

We can easily install SageMath through our Linux distribution's package manager, so let's use that.

First, we'll need to install it:

sudo apt install sagemath

Install the sagemath package and all of its dependencies.

Then launch the sagemath console with the following command:

sage

Let's begin by importing some Python libraries we'll need later:

import codecs
import binascii

Then we'll load all of the known values provided by the challenge. We can begin with the contents of msg.txt:

msg = "Our flags are encrypted and classified, but the messages containing them can be declassified. For example, if we wanted to share this message, we have to remove the flag, like so: XXXXXXXXXXXXXXXXXXXX"

Since we can't perform calculations on the text contents of a string, we'll need to convert the message text to something more usable.

We can convert it to an integer value with some intermediary steps:

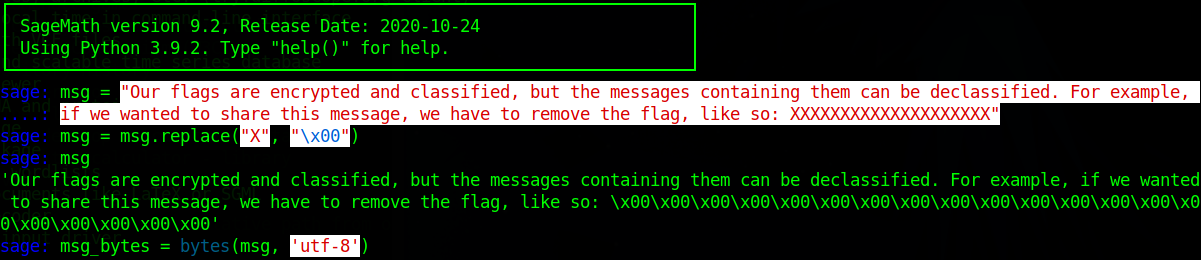
msg = msg.replace("X", "\x00")
msg_bytes = bytes(msg, 'utf-8')
msg_hex = codecs.encode(msg_bytes, 'hex')

First convert the value of msg to a byte string. The byte string can then be converted to hex, which can then be converted to a 16 bit integer value.

These statements should appear similarly in your sage console:

Once those statements have been submitted, the final command should produce the following integer value:

13800504077331705901477337994607819047475992195861970964827502891445436123448264909577010172130234615613798685342009246192219410400007425022836505929195955716740385063998093643952267022760901840799621964297350006245196147907987955260638447653566886598097983651848874527771223121237180250112808277083857650876661838624794010524749867686729177578866744987397048100107832912434669985928163393502645655220354028222387341233791821104219770213676217740879740116078869604084695643434516480

Next, enter the modulus and exponent values from the pub.key file. These will be stored in the n and e variables.

The exponent value is simply:

e = 7

However, the modulus value is provided in hexadecimal:

Modulus:
  00:cc:4f:1e:56:4f:e2:d7:bf:10:dd:25:7c:24:ff:
  37:d0:de:c6:ba:c7:be:df:b2:a8:4f:cc:ed:97:c2:
  0b:58:14:aa:fd:ce:fc:02:07:f1:e6:73:03:d6:15:
  c3:39:fd:17:0b:e4:c3:7c:26:3b:49:fd:87:17:85:
  88:94:67:e9:4d:ed:ea:96:7e:75:26:1d:bf:d8:78:
  2c:08:71:ab:32:68:18:21:bd:b2:94:f8:ae:40:30:
  5d:4b:dc:82:b6:d8:e2:dc:9c:4f:27:dc:89:20:5f:
  99:1f:64:6b:c5:dd:ce:5c:45:46:8e:82:bc:19:9f:
  46:9a:27:11:91:81:b6:70:db:7b:3e:a1:16:1e:87:
  69:19:3a:2d:bd:e2:22:fe:93:32:76:3c:92:b7:25:
  fc:98:1e:34:23:b2:f6:e3:f5:b3:21:ff:5d:53:a0:
  c0:67:ce:c9:e4:6b:73:78:86:a3:f5:e0:80:e4:88:
  82:e4:dc:ff:7b:31:dd:fe:7f:35:02:59:30:f7:fc:
  85:d6:e0:e8:6a:e0:18:97:ae:7a:08:a9:f8:7f:13:
  f3:dc:e3:94:76:50:d9:fa:72:d0:0c:8c:3b:29:df:
  2f:ce:16:b2:3b:0c:0f:e1:5c:53:08:c9:ae:d4:f1:
  cf:14:e0:86:ff:7f:df:99:df:03:72:4d:27:86:b5:
  93:a7

You can use a text editor, like Notepad++, to remove all of the colon and newline characters.

Assign the resulting string to the variable n:

n = "00cc4f1e564fe2d7bf10dd257c24ff37d0dec6bac7bedfb2a84fcced97c20b5814aafdcefc0207f1e67303d615c339fd170be4c37c263b49fd871785889467e94dedea967e75261dbfd8782c0871ab32681821bdb294f8ae40305d4bdc82b6d8e2dc9c4f27dc89205f991f646bc5ddce5c45468e82bc199f469a27119181b670db7b3ea1161e8769193a2dbde222fe9332763c92b725fc981e3423b2f6e3f5b321ff5d53a0c067cec9e46b737886a3f5e080e48882e4dcff7b31ddfe7f35025930f7fc85d6e0e86ae01897ae7a08a9f87f13f3dce3947650d9fa72d00c8c3b29df2fce16b23b0c0fe15c5308c9aed4f1cf14e086ff7fdf99df03724d2786b593a7"

Convert the hexadecimal to integer:

n = int(n, 16)

The following integer value should now be assigned to n:

25791629001754597077614094225076992199010209576122755817752421774318732096753384038208339095159385599394382288981372149991169920071653970823882027438233842487171682655729010378380311251486810962185242309623547930621345275554645653875327683522045059140333256348541725154308928882122821848211865614708724559906453390356640305803087086363768767676296142910066431605792016691669827414089369906703119813698697793022970882650146438373426039489521858523361154764663911563981839974855184732308408749223042530935718593438975800375873630129868144557420244609094373728818690154884524238804920574413721070097326355468872276349863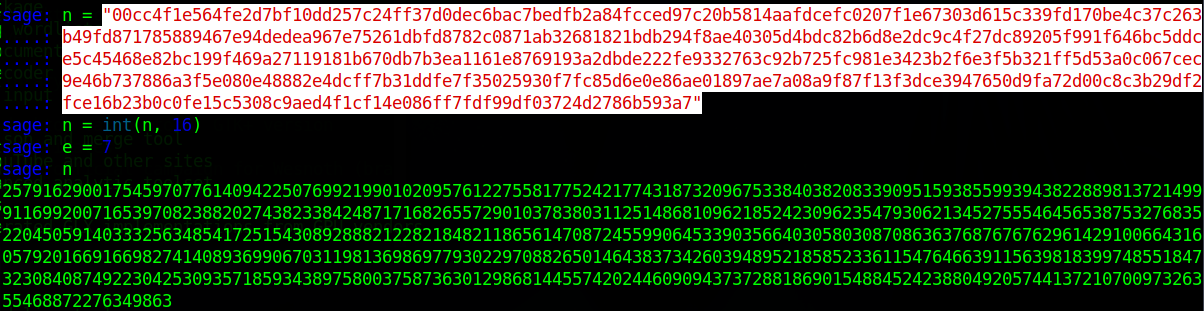

Next, we'll need to get the integer value of the encrypted message and assign that value to the variable c.

Do this by reading the binary contents of the file and storing that in a variable:

fh = open('enc_msg.txt', 'rb')
content = fh.read()

Then convert the value of content to hex. We could do this with codecs.encode(), as we did with the plaintext message, but let's use binascii.hexlify() this time:

content_hex = binascii.hexlify(content)

The value of content_hex should be:

b'9f0e6ed5ebec1fbf634e4a8f8369589a1c459d4b72cf06fb689cac81e250908e25cc6ac5e440e977a5cf85db4abd52ec7d9f86d4c0fde5f74249b71bede9a9e0bd827611ffe0acabc7eefe3eb65f5d6c19c28d8ffe7a513162c5ed658b872ced5fcd1dc8e60270eb77563f48287163701d2d3b9956b515c43283c5d8d6f97baabdb38d490b060787540533e64b1a8a0ebad3870afd12142ffc5c2fb78c6f832d24c93833812a01604c8d18979fc149e4e4490c91724ce8465e4f7b3b5b8c7a13e363393232fcd95e420d57241bef3d1a22ae1f0cf2f02ec063ea4831a058a9264bf4d93686a8c4df11f7289d5b6a6cf9a90eb0608d3f1b84b050c2f09709520b'

Then convert it to integer and assign it to the variable c:

content_int = int(content_hex, 16)
c = content_int

The value of c should now be:

20079007643338722096035115368444030096934434701217379311137953420554141592445556053213376588072736573765933627304841736832576979356711511459466808125182537593650559456478506458673135796540045501403738894971035301447346479139977213636507288802514886263359418058597001914039829087439327312816981659544318823598677262969501262747459661353839173357380859610072012536930386881455042752048538148614921845742342015451126110689830475333025121614973349190101602304647828912307493938102500924722246658122151514433784568039109239110878548160165669575436481704927756033049855791309263552415215560247433040916876342094582816264715

At this point, we're finally ready to begin executing Coppersmith's Method.

The first thing we'll do is create a Polynomial Ring object using the modulus value:

P.<x> = PolynomialRing(Zmod(n))

Next, we'll setup the function for which the roots will be computed. Before we do that, it's worth referring to Coppersmith's Theorem for some awareness of what we're doing:

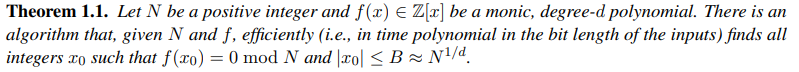
Which is a particular application of the RSA function:

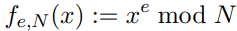
In fact, the function we create will be very similar to the RSA function.

Since most of the contents of msg.txt are known to us, we can add that value to x in the function:

f(x) = (msg_int + x)e mod N

Coppersmith's Method equates the value of the encrypted message to the value of the known and unknown message.

Since we're searching for the roots, we can subtract the encrypted message value from both sides:

    c = (msg_int + x)e mod N

​   0 = (msg_int + x)e -c (mod N)

Then divide both sides by (mod N), and we'll have the following function:

    f(x) = (msg_int + x)e - c

Enter that into the sage console, and also apply the monic() method, and finally use the small_roots() method:

f = (msg_int + x)^e - c
f = f.monic()
m = f.small_roots()

That should complete fairly quickly, but...we don't get a solution. The value of m is an empty list:

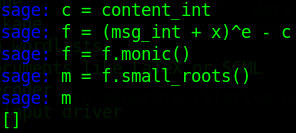
Let's try executing the small_roots() method again, except this time we'll set a value for the epsilon argument. Set the value of epsilon to 1/50.

m = f.small_roots(epsilon=1/50)

This calculation will take some time, but it will result in a single-element list:

Convert the value of that element to hex:

decode_hex = hex(int(m[0]))

Which should result in the following value:

'0x6374667b736d317468316e675f6330707033727d'

This is the value redacted portion of msg.txt...the flag.

Convert this to text in order to reveal the flag.

You'll need to skip the first two elements of the string, which can be done with a string slice beginning at index 2.

decode_hex[2:] 
'6374667b736d317468316e675f6330707033727d'

Use the bytes.fromhex() function and the decode() method to get the flag:

print(bytes.fromhex(decode_hex[2:]).decode('utf-8'))

This should print the flag: ctf{sm1th1ng_c0pp3r}

References:

https://medium.com/@hva314/some-basic-rsa-challenges-in-ctf-part-2-applying-theoretical-attack-55a2cc7baa11

https://medium.com/@hva314/some-basic-rsa-challenges-in-ctf-part-1-some-basic-math-on-rsa-5663fa337c27

https://github.com/hva314/backdoorctf2017/tree/master/stereotype

https://github.com/ashutosh1206/Crypton/tree/master/RSA-encryption/Attack-Coppersmith/Challenges/stereotypes

http://web.archive.org/web/20201101235721/https://hva314.github.io/blog/2017/09/24/Backdoor-CTF-2017-Crypto.html

https://web.eecs.umich.edu/~cpeikert/lic13/lec04.pdf

https://stackoverflow.com/questions/3116907/rsa-get-exponent-and-modulus-given-a-public-key